Undersite für das schulübergreifende Wahlpflichtfach Mathematik im Schuljahr 2018/19

Wien, im Jänner 2018.
Liebe matophile junge Damen und Herren! :-)
Willkommen auf eurer undersite. Jene besteht momentan lediglich aus dem Anmeldeformular, welches ihr mir bitte ausgefüllt und gescannt per e-mail schickt. Ab Herbst 2018 wird sie dann ähnlich bestückt wie die anderen über www.matheprof.at einzusehenden WPF-Undersites, wobei an dieser Stelle jetzt schon verraten sei, dass (aktualisierter Stand vom 12.4.2018) zwei Damen und neun Herren an diesem schönen WPG teilnehmen werden, und zwar aus acht verschiedenen Schulen, welcher ihrerseits wiederum über fünf Bezirke (Leopoldstadt, Landstraße, Josefstadt, Hietzing, Donaustadt) verteilt sind.
Anmeldeformular für 2018/19(/20/21)
NEWS: Kriterien der Leistungsbeurteilung
"Klassenbuch":
NEU: Blockungstermine für das Sommersemester 2019 (Änderung via 13.2.!)
Jeweils von 16.25 bis 18.55 findet das WPF mit
Ausnahme des 21.2,. 4.4 und 11.4. (Abwesenheit des Kursleiters wegen
Administratorenausbildung bzw. Mathematikolympiade-Gebietswettbewerb) sowie des
13.6. (mündliche Matura) zu den folgenden Terminen statt:
Änderung: Trotz der
Termine am 21.2. und 11.4. findet das WPF mit bemühter Pünktlichkeit des Leiters
statt (bemüht wegen der Anreise!).
Do, 14.2.2019: Teil 2 von Thema VI und komplettes Thema VII: Trigonometrie
Do, 21.2.2019: Thema VIII: Dreiecksgeometrie, Teil 1 (einleitend zur Ergänzung von Pool-Thema VIII: Schwerpunktformel)
Do, 28.2.2019: Teil 2 von Thema VIII sowie enreut zur Ergänzung von Pool-Thema VIII: Inkreismittelpunktformel (Beginn)
Do, 7.3.2019: "Ozean"-Thema "Inkreismittelpunktformel" (Fortsetzung und Abschluss) sowie (2/3 des Triple features) Fragestunde zu "Los prüfos" am 14.3.2019
Do, 14.3.2019: "Los prüfos" aka Probematura (Respekt vor den guten Leistungen!)
Do, 21.3.2019: Freie Ozeanmathematik IV, V und VI (nach dem 27.9., 21.2. und 28.2./7.3.): Satz über arithmetische Dreiecke, Fegerlsche Summationsmethode sowie (in Anlehnung an Kapitel 3.2 dieses Buchs) Beginn mit der Sinnfrage nach dem Winkel zwischen Gerade und Ebene (wobei wir anders als dort wegen Relja, Nicolas und den Bernoulli-Boys keine Differentialrechnung verwenden werden ...)
Do, 28.3.2019: Abschluss von freier Ozeanmathematik VI (Sinnfrage nach dem Winkel zwischen Gerade und Ebene), freie Ozeanmathematik VII (Approximation von Quadratwurzeln via sukzessiver Quadratur - was zum Heron-Verfahren führt - sowie via Kettenbrüche), Teile VIII bis ??? dann 2019/20 im Bernoulligymnasium
entfällt aufgrund der mehrmaligen Überziehungen (vor allem am 14.3.): Do, 11.4.2019 (nur mehr zweistündig, da ja auch bereits am 31.1.2019 geblockt wurde!), WOMIT WIR NUN MIT 28.3.2019 für ein knappes halbes Jahr pausieren ...
Da 8∙3=12∙2 gilt, entfallen daher die vier Termine am 9.5., 16.5., 23.5. und 6.6.2019. Dann heißt es für euch:

;-) Wir wissen ja, dass Mathematiker keineswegs so aussehen und können dies bei Lust und Laune durch ein Erinnerungsfoto (Da hat Sinushi womöglich schon längere Haare ...) gerne aushebeln, welches nunmehr mit zweimonatiger Verspätung via 1.5.2019 folgt ...

..., wobei v.l.n.r auch entsprechende Codenamen "verraten"
werden:
Sinushi, Realistische, Francoise, Student, Bahnsteiger, Berti, Danger zone
(leider beim Fototermin krank: Timberfriend)
Themenbereiche für die mündliche Reifeprü-fung (Übersicht bzw. detailliert, ACHTUNG: Die Themen 6 bis 9 wurden FÜR DIE MÜNDLICHE MATURA aus dem Pool ent-fernt, womit ACHT THEMEN FÜR DIE MATURA und somit auch DIE PROBEMATURA IM JÄNNER 2019 bleiben, nämlich 1 bis 5 sowie 10 bis 12), was zu 50% durch die Abschnitte ...
3.3.3 (Teil von Thema 2),
2.1.11 (Teil von Thema 3), 2.1.1 und 2.1.4 (beide zu Thema 4, wobei 2.1.4 im WPF
ausführlicher durch-genommen wird als im Buch), 2.2.1 und 2.2.4 (beide zu Thema
5, wobei 2.2.1 im Buch ausführlicher durchgenommen wird als im WPF), 4.1 (Teil
von Thema 7), 4.16 (Teil von Thema 8), 2.15 und 2.16 (beide zu Thema 10) sowie
last but not least 3.9 (zu Thema 12) des links abge-bildeten Buchs abgedeckt wird
(dessen Erwerb aber keinesfalls eine notwendige Bedingung für ein erfolg-reiches
Absolvieren dieses WPFs darstellt, sondern lediglich für besonders Interessierte
viele weitere faszinierende mathematische Themen beinhaltet) ...
...
und zu weiteren beinahe 30%
durch die Abschnitte 5.1.11 (Teil von Thema 1), 4.4.2 (Teil von Thema 2), 5.1.7
(Teil von Thema 6), 5.2.5 (Teil der Themen 3 und 6) sowie 5.11.1 und
5.11.3 (beide zu Thema 11) des links abgebildeten Buchs abgedeckt wird (wo-bei freilich auch dessen Er-werb
ebenso wenig eine notwendige Bedingung für ein erfolgreiches Absolvie-ren dieses WPFs
ist, son-dern lediglich für besonders Interessierte
viele weitere faszinierende mathemati-sche Themen bietet).
Ferner
wird der im ersten Buch fehlende Teil von Thema 7 im links abgebildeten Buch
behandelt
(wobei natürlich ebenso dessen Erwerb erneut keine notwendige Be-dingung für ein erfolg-reiches Absolvieren dieses WPFs
ist, son-dern lediglich für beson-ders Interessierte
viele weitere faszinierende mathematische Themen bietet).
Schließlich wird der zweite Teil von Thema 8 im Buch "Von der Addition bis zur z-Koordinate" behandelt, welches ab Anfang Jänner 2017 im Handel unter obiger ISBN-Nr. erhältlich sein wird.
Damit bleiben mit einem Teil von Thema 1 sowie komplett mit Thema 9 nur 3 von 24 Teilthemen "übrig", welche in keinem der vier Bücher behandelt wer- den. 12 bzw. 7 resp. 1 sowie 1 Thema/Themen werden somit durch das erste bzw. zweite resp. dritte sowie vierte Buch abgedeckt. Thema 9 und der feh-lende Teil von Thema 1 sind für das fünfte Buch schon zu 100% eingeplant.
Nähere Informationen zu diesen vier Büchern findet man gesammelt hier (ferner detailliert UND REZENSIERT für Buch 1 und Buch 2) oder auch gerne beim Autor persönlich! Ferner sind alle* Bücher in der Schulbibliothek der AHS Heustadelgasse entlehnbar.
*Nr. 4 erst i.L.d. Jänners 2017
NEU (3. 2. 2014): Video zum Oktaederstumpf
Bezüglich anderer Themen (bzw. deren Anregung):
Links zu den Wahlpflichtfachseiten früherer Jahre:
für ALLE WIENER GYMNASIEN)
Mit freundlichen Grüßen
Dr. Robert Resel
P.S.: 1) Schließlich noch eine singuläre Anregung:
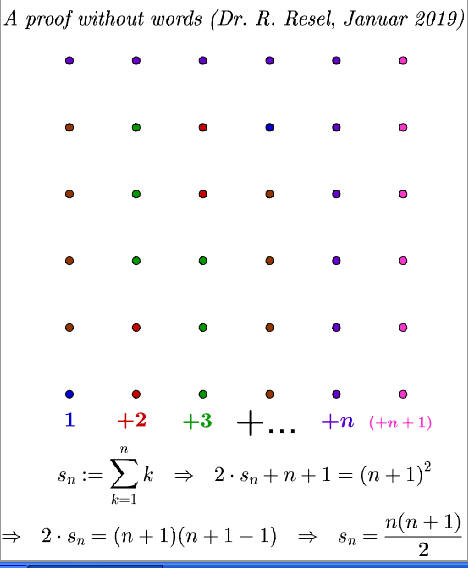
Erkläre den obigen äußerst ungewöhnlichen Beweis des Lehrsatzes von Pythagoras!
2) bis ???): Weitere Anregungen
2) Goldener Schnitt (F,1/F,F²,...)
3) Forschen in der Geometrie (mit der dynamischen Software GeoGebra): Forschungsprojekte 1 und 2