
Undersite für das Wahlpflichtfach Mathematik
(8B/8C/8D, Schuljahr 2011/12)
Wien, den 12. Juli 2011.
Werte angehende Wahlpflichtfachlerin, geschätzte WahlpflichtfachlER!
101) Addieren und Subtrahieren wiederholen!
102) Multiplizieren und Dividieren wiederholen!☺
103) Differenzieren wiederholen und sich aufs Integrieren freuen! <3
Und "jz" kommt´s:
I)

II)

III)

IV)

V) ... Fortsetzung/Ausbau der Vektoralgebra
(Grassmannsche Entwicklungssätze, Jacobi-Identität)
von 2010/11: Herleitung (folgt im WPF!) von ...

VI) ... nur dass wir es im WPF-M bei den folgenden
Volumsformeln nicht beim Nachrechnen belassen (sic!) ...


VII) ... auf in höhere Dimensionen ...
VIII) ... dazu zunächst eine Auffrischung aus der dritten Dimension:
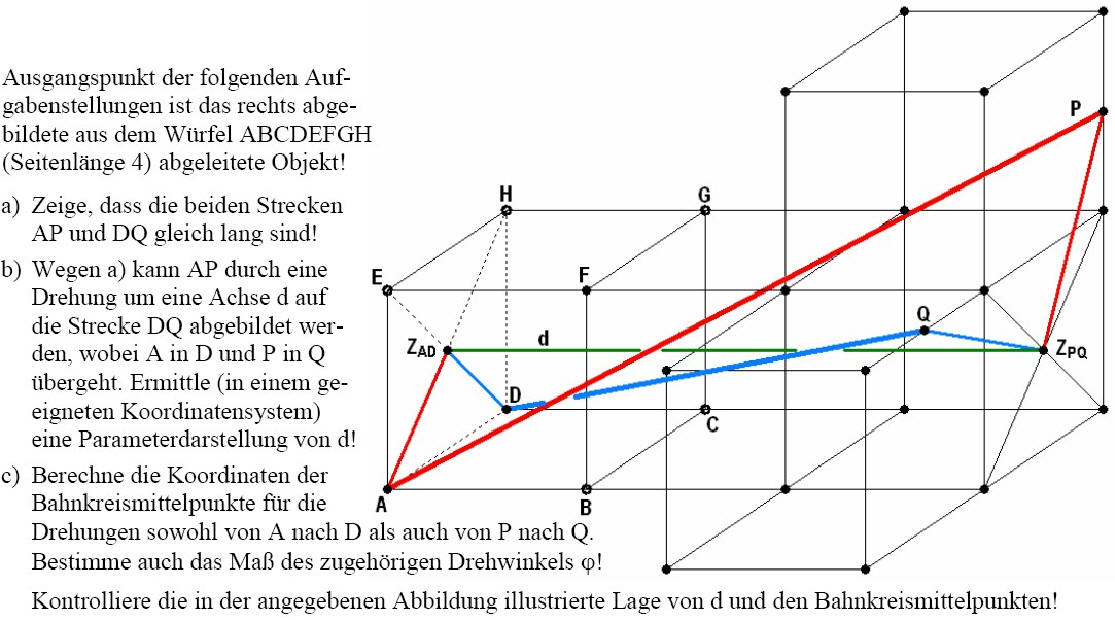
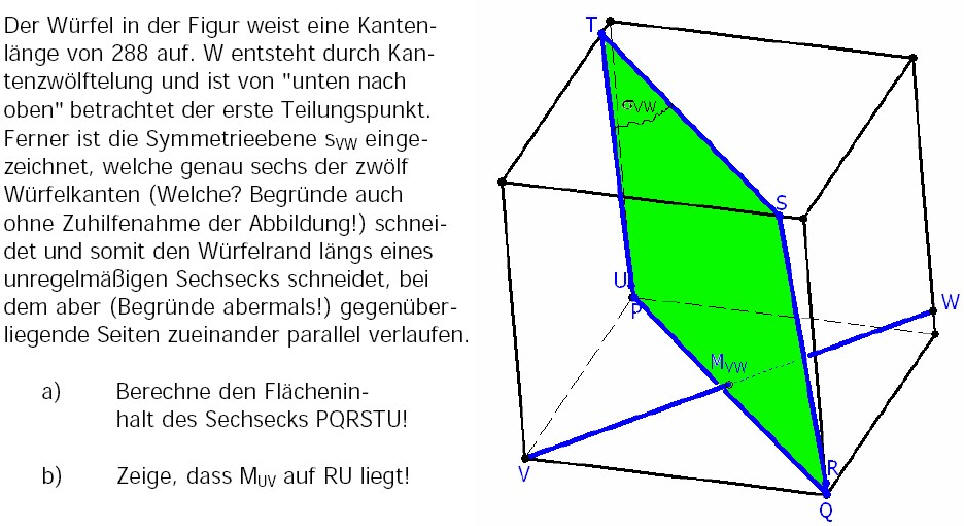
IX) Nachschlag (auch als pdf-file!) zu den Kegelschnitten (hier freilich zum BEWEIS!), ferner ...
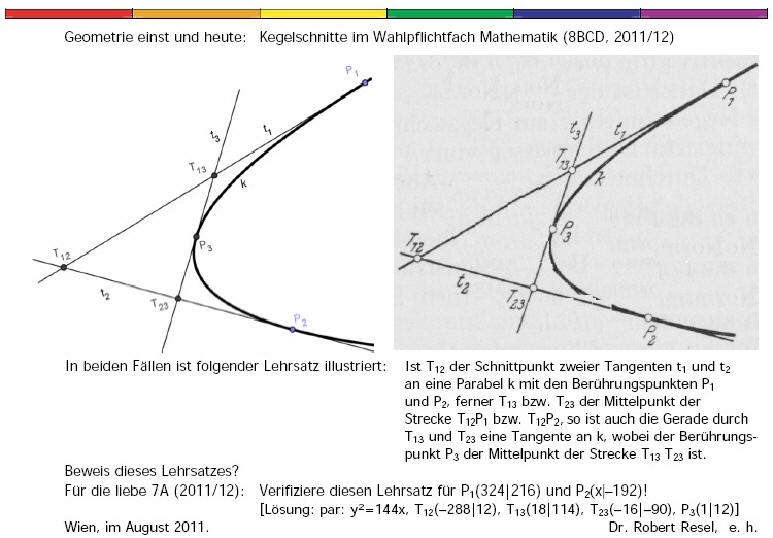
... anschließende äußerst praktisch ausgerichtete und im WPF zu erörternde Frage, wie man vorgeht, um die linke GeoGebra-Grafik der rechten gute 60 Jahre alten Abbildung möglichst genau nachzuempfinden
(Hinweis!)?!?
Legt man auf den Brennstrahl b eines beliebigen Parabelpunkts P die Normale n durch P, schneidet sie mit
der Parabel par (par∩n={Q}) und ermittelt ferner den Schnittpunkt R der Tangenten tP und tQ, dann gilt:
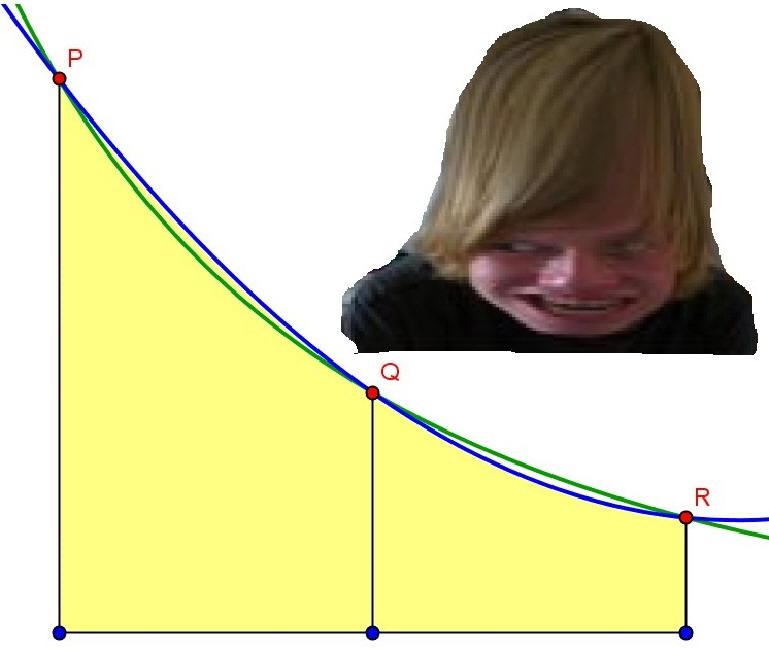
XI) Bekommst du es mit der Angst zu tun, wenn du bestimmte Integrale schwieriger Funktionen zu berechnen hast (und/oder Meister Eder in solch horrribel verzerrter Form sehen musst☺)? Dann greife zu einem Hilfsmittel aus der Numerischen Mathematik, nämlich der Kepler-Regel!
XII) Eine tiefergehende Analyse numerischer Verfahren wird erst durch die Taylor-Formel möglich, welche auch ...
XIII) ... auf das Newton-Verfahren angewandt wird sowie ...
XIV) ... auf Summensätze der Winkelfunktionen,. ...
XV) ... einen (bereits bekannten, aber bislang wohl im Unterricht unbewiesenen!) Extremwerttest ...
XVI) ... und schließlich die "69er-Regel" u.ä. aus der Finanzmathematik!
Weitere Möglichkeiten:
XVII) Differentialgleichungen
XVII) Differenzierbarkeit im Komplexen
(Cauchy-Riemannsche Differentialgleichungen)
XXIX) Integration von Kurven in Parameterdarstellung (Sektorformel, Kurvenintegrale)
XX) Die Eulersche Formel eix=cosx+i·sinx
XXI) Der Fermatsche Punkt eines Dreiecks
XXII) Höhere Momente stetiger Zufallsvariabler (Schiefe und Exzess)
XXIII) Bogenlängenberechnungen mittels bestimmtem Integral
XXIV) Mantelflächeninhaltsberechnungen mittels bestimmtem Integral
XXV) Schwerpunktsberechnungen ebener Gebiete via best. Integral
XXVI) Schwerpunktsberechnungen von Drehkörpern via best. Integral
XXVII) Winkeltreue konformer Abbildungen
XXVIII) Die Analysis hinter der Normalverteilung
XXX) Mehr über den Lehrsatz des PYTHAGORAS in 3D!
XXXI) Zusatz zu I):

XXXII) Zusatz zu V):

Mit freundlichen Grüßen
Dr. Robert Resel